Dropout
- 3 minsDropout
그놈의 over-fitting!
딥러닝 모델 개발을 조금이라도 심도있게 해본 개발자라면 over-fitting이란 단어에 매우 친숙할 것입니다. over-fitting이란 딥러닝 모델이 다양한 요인들로 인해 학습데이터를 과하게 학습하여 학습데이터와 유사한 다른데이터에 대해서는 성능이 좋지않은 현상을 말합니다. 자세한 내용은 포스팅 regularization의 서두에서 다루었습니다.
이런 over-fitting을 해결하게 위해 현재까지 다양한 방법들이 개발되었습니다. Dropout은 딥러닝의 태동기 때부터 사용되었던 over-fitting해결방법으로써, 간단하게 설명하면 딥러닝 layer를 연결하는 각 node를 랜덤하게 사용하지 않고 데이터를 학습하는 방법입니다. 딥러닝을 처음 접하고 배우고 계신분들은 이런 방식이 왜 모델의 성능을 올리는지 이해가 되지 않을 것입니다. 자세한 내용은 본문에서 다루겠습니다.
이번 포스팅은 아래와 같은 순서로 진행합니다.
- Dropout
- Effect of Dropout
- Type of Dropout
- 정리
- reference
1. Dropout
Dropout은 deep learning기법의 태동기에 개발된 기술로 당시에는 under-fitting의 문제도 있었지만 동시에 over-fitting에 대한 이슈가 많았습니다. 그래서 ‘복잡한 딥러닝 모델을 오히려 간단하게 만들면 성능이 증가하지 않을까?’라는 가정에서 개발된 기술로, 딥러닝의 대가인 Geoffrey Hinton교수에 의해 JMLR, 14년에 처음으로 제안된 기술입니다. (추가내용으로 해당 논문의 편집자로 무려 딥러닝의 또 다른 대가인 Yoshua Bengio교수도 참여했습니다. 그렇기에 기술뿐만아니라 좋은 논문 작성법을 익히고 싶은 개발자라면 한번 쯤은 정독해볼만한 좋은 논문입니다.)
Dropout은 ‘딥러닝 기법은 복잡하고 수많은 parameter들로 구성된 모델을 이용하여 어떤 값들을 추정 및 예측하는 기술인데, 더욱 복잡하고 많은 parameter를 사용했기에 over-fitting이 발생하지 않을까? 그러면 모델을 반대로 간소화하는 방향으로 학습하면 성능이 오히려 좋아지지 않을까?’라는 가정에서 시작된 기법으로, 각 layer를 연결하는 node들을 무작위하게 끊으면서 학습하는 기법입니다. 아래의 그림은 dropout을 간단하게 구현한 그림입니다.
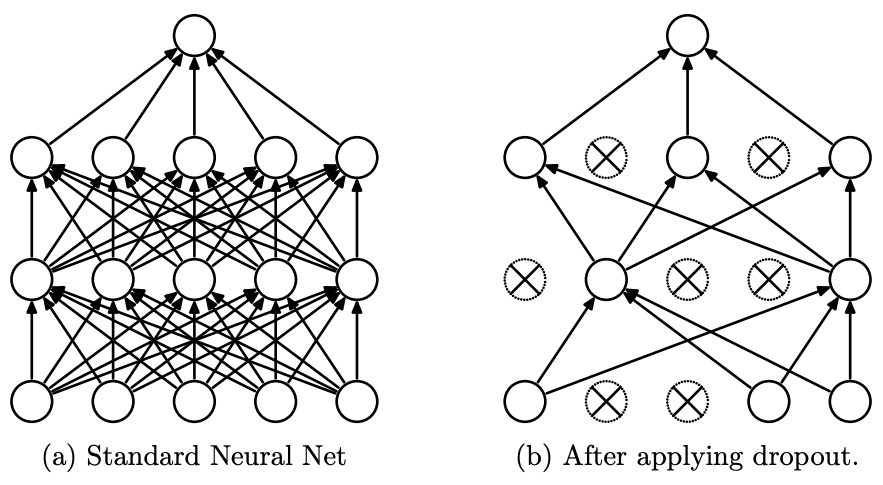
그러면 Dropout이 정확하게 어떤식으로 모델학습에 사용되어 모델의 성능을 올리는지 알아보겠습니다. 아래의 수식을 보면서 설명하겠습니다. 먼저 \(l\)은 hidden layer, \(w\), \(b\)는 각각 weight, bias를, \(z\), \(y\)는 각각 layer의 input, output이며, \(f\)는 activation function을 의미합니다. 예를 들어 \(w_i^{l+1}\)은 \(l\)+1번째 layer의 i번째 weight를 의미하며 \(y^0\)은 첫번째 layer의 input을 의미합니다. 기존의 model의 경우, 이전 layer의 output과 weight, bias조합으로 다음 layer의 input값을 계산하고 여기에 추가로 activation function을 통해 다음 layer에 얼마만큼의 영향을 줄것인지 결정합니다.
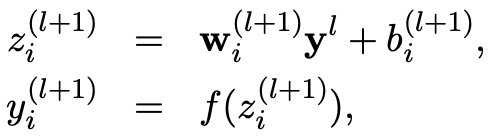\(z_{i}^{l+1} \quad=\quad w_{i}^{l+1}y^{l} + b_{i}^{l+1}\) \(y_{i}^{l+1} \quad \sim \quad f(z_{i}^{l+1})\)
여기에 dropout기법을 적용하면 기존 모델의 output \(y\)에 어떠한 분포도를 따르는 인자를 생성하는 방식을 사용하거나 혹은 randomly hard decision방식을 사용하여 생성한 parameter \(p\)를 적용한 \(\widetilde{y}\)을 해당 layer에 적용합니다. 추가적으로 parameter \(p\)를 어떤방식으로 생성하느냐에 따라 다양한 dropout기법이 추가적으로 존재합니다.
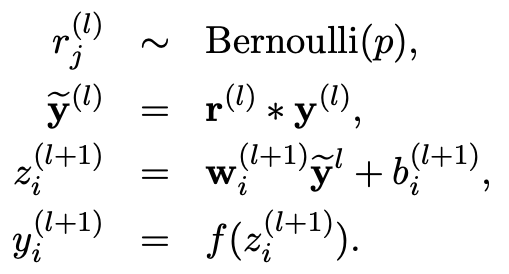\(r_{j}^{l} \quad \sim \quad Bernoulli(p)\), \(\tilde{y}^{l} \quad=\quad r^{l}r^{l}\), \(z_{i}^{l+1} \quad=\quad w_{i}^{l+1}\tilde{y}^{l}+b_{i}^{l+1}\), \(y_{i}^{l+1} \quad=\quad f(z_{i}^{l+1})\)
위의 dropout기법의 수식을 하나의 layer에 적용하여 간소화하면 아래의 그림과 같습니다.
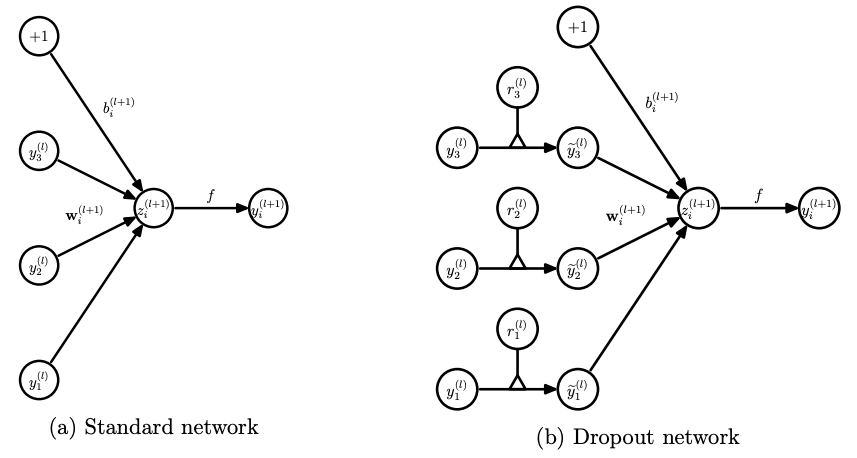
inference
앞서 설명한 dropout방법은 그대로 training step에 적용하면 된다. 그렇다면 inference step에서는 어떤방식으로 적용될까? training step에서 각 layer에 적용한 \(p\)값을 hyper-parameter로 저장해뒀다가 inference step시, 각 layer의 node에 training step과 동일하게 적용하여 inference를 진행합니다.
2. Effect of Dropout
장점 :
- Dropout은 매 epoch의 feed-forward과정마다 node를 사용하지 않고 학습하기 때문에 필연적으로 back-propagation과정에서도 동일하게 학습이 되지 않습니다. 그렇기 때문에 매 epoch마다 새로운 모델을 학습하는 효과를 가져오며, 최종적으로 weighted sum을 통해 concat하여 모델을 구성하기 때문에 ensemble기법이라고도 불리웁니다.
- fully connected layer에서 학습을 통해 특정 node들의 관계만 강해지는것을 방지합니다.
단점 :
- fully connected layer에서 특정 node들을 사용하지 않으면서 학습을 하기 때문에, 수렴이 늦어질수 있고 데이터와 모델의 특성에 따라 성능이 떨어질수도 있고 training error가 다소 증가할 수도 있습니다.
- hyper-parameter가 증가합니다.
3. Type of Dropout
-
fast-dropout : 위의 단점을 개선하기 위해 개발된 기법으로, dropout의 학습속도가 느린 이유는 매 epoch, layer마다 새로운 p를 생성하여 학습하기 때문입니다. 그래서 어차피 수많은 p를 생성하게 되면 gaussian distribution을 따르게 되는데 그러면 처음부터 gaussian distribution을 따르는 p를 모든 layer에 미리 적용한 뒤에 학습을 하는 기법입니다.
-
DropConnect : Basic dropout의 경우, 각 node들의 연결을 무작위로 끊는 방식으로 학습을 합니다. Dropconnect은 node가 아니라 각 layer의 weight를 0으로 만드는 방식으로 학습을 진행합니다. Dropout의 경우에는 단순히 node들만 끊으면서 학습하나 dropconnect의 경우에는 딥러닝 모델의 가장 중요한 parameter라고 할수 있는 weight만 학습에 영향을 준다는 측면에서 dropout보다 조금 더 일반화적인 학습방식이라고 볼 수 있습니다.
4. 정리
이번 포스팅에서는 dropout에 대해 설명하였습니다. 이번 포스팅을 요약하면 dropout은 학습때 임의의 node들을 삭제하면서 학습하는 기법이다. 이것과 부수적인 내용만 확실하게 아셨으면 이번 포스팅을 훌륭히 이해하신겁니다.
5. reference
[1] Dropout: A Simple Way to Prevent Neural Networks from Overfitting