Optimizer
- 11 minsOptimizer
hyper-parameter를 어떻게 업데이트 할껀데?
이번 포스팅에서 다룰 기술은 바로 Optimizer입니다.
좋은 딥러닝 개발자가 되기위해서는 기본적인 딥러닝 구조를 기초부터 알아가는 과정이 매우 중요합니다. 딥러닝 모델로 데이터를 입력받아 각각의 layer를 통과하고 cost function을 통해서 cost를 감소시키면서 optimizing, back-propagation을 통해 학습데이터에 맞게 모델을 조정하는 과정이 딥러닝 모델 학습의 대략적인 과정이라고 할 수 있습니다.
그러면 여기서 의문점. 그래서 cost는 어떻게 감소시키는데?
여기서 사용되는 알고리즘이 바로 Optimizer! Optimizer는 딥러닝에서 중요한 부분중의 하나인 cost를 줄이는 과정을 담당하고 있으며 좋은 딥러닝 개발자가 되기위해서 기본적으로 알아야할 알고리즘 중에 하나이기에 이번 포스팅의 주제로 선정하였습니다.
이번 포스팅은 아래와 같은 순서로 진행합니다.
- What is optimizer?
- Gradient descent
- 문제점
- optimizer의 종류
- 최신 optimizer 및 이슈
- 정리
- reference
1. What is Optimizer?
딥러닝을 처음 접하는 초심자들을 위해 간단한 비유를 한다면 필자는 종종 데이터를 몸, 딥러닝 모델을 옷에 비유하곤 합니다. 여기서 optimizer는 옷을 수선하는 방식이라고 생각하면 편할 것같습니다.
데이터(몸)에 맞는 딥러닝 모델(옷)을 만들기 위해서는 딥러닝 모델의 layer와 이외의 알고리즘에 존재하는 hyper-parameter를 데이터에 맞게 최적화 해야합니다. 그래서 supervised learning을 기준으로 설명하면 target data(견본 옷)가 존재하고 input data(몸의 실루엣)가 존재하면 딥러닝 모델을 통과한 input data와 target data의 사이의 오차를 계산하는 cost function을 먼저 결정하고 이러한 cost function의 cost(오차)를 줄이기 위해 hyper-parameter를 수정해야 하는데 여기서 사용되는 것이 바로 optimizer입니다. 대략적으로만 살펴봐도 optimizer가 모델 성능에 지대한 영향을 끼칠 것을 알 수 있습니다.
요약 : cost function과 hyper-parameter을 통해 모델이 최적의 성능을 낼 수 있도록 cost가 감소하는 방향의로 hyper-parameter를 업데이트 해주는 알고리즘
2. Gradient Descent
위키피디아에 gradient descent를 검색하면 “In mathematics gradient descent is a first-order iterative optimization algorithm for fining a local minimum of differentiable function.”이라고 나옵니다. 직역하면 “미분가능한 함수의 극소값을 찾는 1차 반복 최적화 알고리즘”입니다. 앞서 설명햇듯, 딥러닝 모델은 학습데이터를 반복적으로 모델에 학습시켜 데이터에 맞게 딥러닝 모델의 parameter를 업데이트하여 데이터에 딥러닝 모델을 최적화하는 방식으로 생성된다고 하였습니다.
(빠른 진행은 위해 앞으로 gradient descent를 GD라 부르겠습니다.)
여기서 반복, 최적을 강조하였듯 이 두가지가 optimizer에서 가장 중요한 키워드라고 할 수 있습니다. 그럼 본격적으로 Optimizer에 대해 이해를 돕기위해 GD에 대해 설명하겠습니다. GD는 매우 기본적이며 이해가 쉬운 방법이기에 대부분의 블로그나 책에서 GD를 예시로 설명하는 것이 바로 그 이유이며 필자도 동일하게 GD를 예시로 optimizer에 대한 전반적인 설명을 하겠습니다.
그러면 본격적으로 GD가 무엇이냐? Gradient Descent, 경사하강법이라고 하는 이 방법은 w를 미지수로 가지는 함수 J(w)를 최소화 하는 방법입니다.
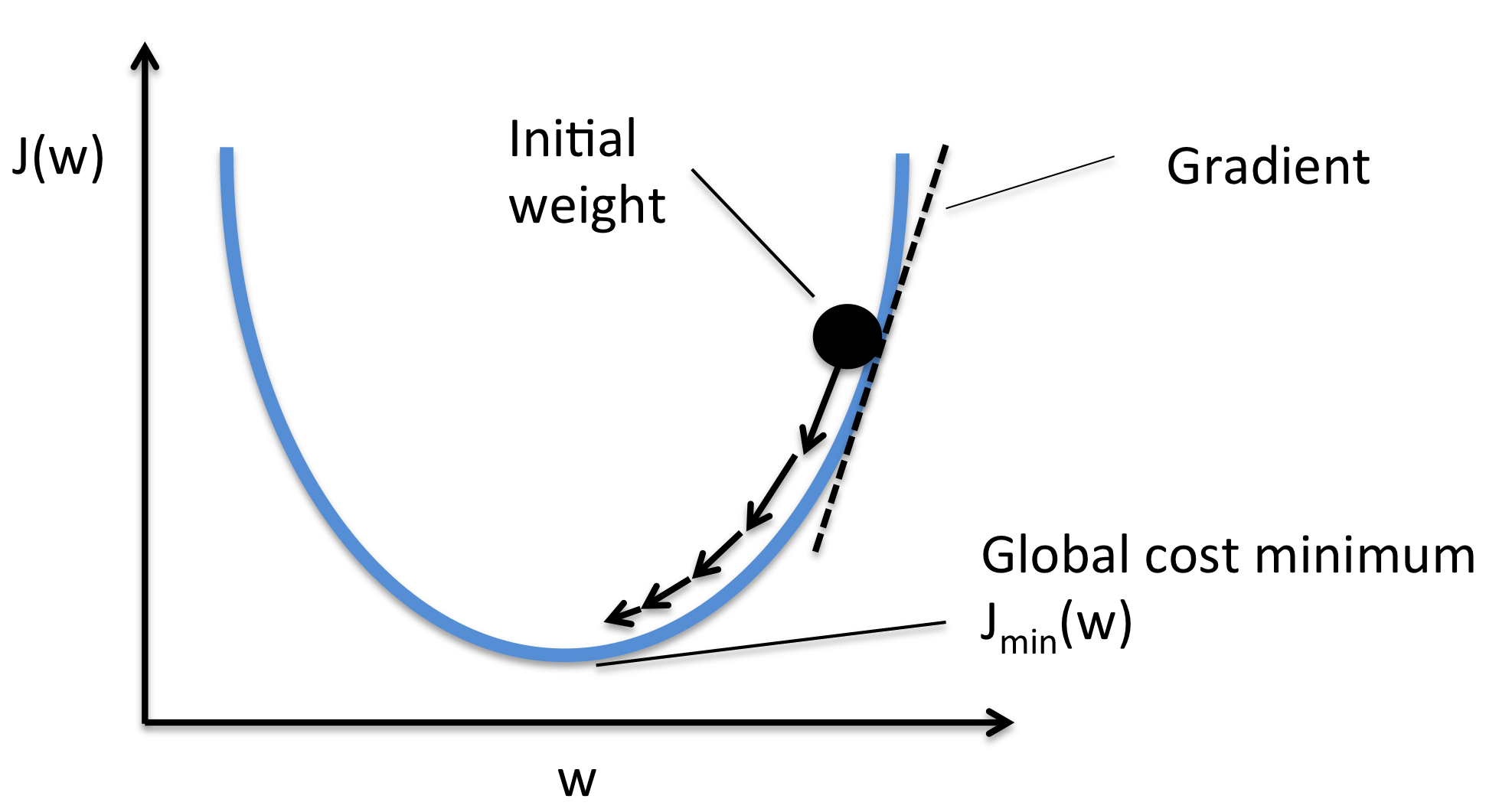
위의 두번째 수식이 cost function입니다. 계속해서 언급했듯, 딥러닝 모델이란 학습 데이터에 모델을 반복적인 학습하여 최적화 시키는 작업이라고 하였고, 최적화라고 할 수 있는 인자가 cost라고 할 수 있으며 이 값을 최소로 만든다면, 딥러닝 모델이 데이터에 최적화 되었다고 얘기할 수 있을 것입니다.
그래서 학습시 cost function에 optimizer를 적용하여 모델 파라미터 수정을 빠르게 할것인지 천천히 진행할것인지 혹은 어떤식으로 조정할 것인지 결정 할 수있습니다.
설명을 간단히 하기 위해 bias를 제외하고 weight와 cost function 두 가지만 가지고 진행하겠습니다. 최초, 초기 weight값(\(w_{0}\))이 존재하며 이를 업데이트 하기 위해서는 learning rate(\(\eta\))와 cost(\(J(w_{t})\)), weight의 미분 값(\(\frac{\partial w}{\partial J}\))을 이용하여 업데이트 해줍니다. 이런식으로 전체데이터에 대해 반복적으로 weight를 조정하면서 데이터에 모델을 최적화 시키는 겁니다. (이런방식으로 bias 이외에도 다양한 hyper-parameter에 대해서도 업데이트해줍니다.)
Q. 최초학습 때, w, b는 어떻게 설정하는데? 초기 딥러닝 모델들은 일반적으로 w,b를 random값으로 설정하여 최초 학습을 시작하였으나 최근에는 초기값으로 0을 설정해도 성능에 크게 차이가 나지 않는다는것이 증명되어 0으로 사용하여도 무방합니다.
3. 문제점
그러나 딥러닝을 조금이라도 경험해본 분들이라면 눈치 챘을 수도 있겠지만, 아무도 GD를 사용하지 않습니다. Why? GD보다 좋은 optimizer가 너무나도 많이 개발되었기 때문입니다.
그러면 GD는 어떤 문제가 있을까요?
첫번째, 학습속도가 매우매우 느립니다.
GD는 단 한번의 파라미터 업데이트를 위해, 모든 학습데이터에 대해 cost를 계산한 뒤에 업데이트합니다.
그래서 이게 왜 문제가 되는데???
GD는 컴퓨터가 개발되기도 전에 나온 이론이고 해당 기술을 머신러닝 목적으로 사용했을 때에도 대략 1940~2000년대에 적용했었습니다. 다시말해 이전에 GD가 사용될 떄는 데이터의 양이 매우 적었고 그렇기에 GD를 적용하는데 아무 문제가 되지 않았습니다. 왜냐하면 얼마되지도 않는 데이터를 쭉 훓어보고 한번 업데이트하면 그만이였으니까요. 그러나 딥러닝에 GD를 적용하는 것은 또 다른 문제입니다. 딥러닝은 기본적으로 무수히 많은 종류와 많은 양의 데이터를 이용하여 모델을 학습하기 때문입니다. 그렇기에 전체데이터를 다 훓어보고 한번 업데이트를 하게된다면 적당한 성능의 모델을 개발하기위해 천문학적인 리소스가 필요하게 될것입니다.
두번째, local minimum에 빠질 수 있다.
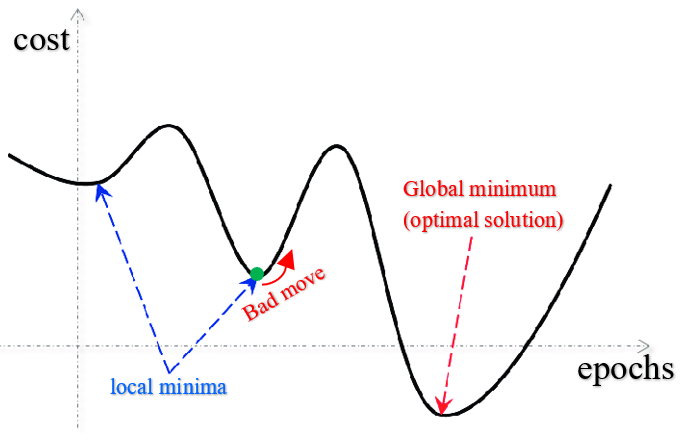
Learning rate를 어떻게 설정하냐에 따라 다르겠지만 일반적인 상황을 가정했을 때, GD는 전체 데이터를 보고 조금씩 weight optimization을 진행하게 되는데, 위 그림에서 알수 있듯이 convex한 부분 근처에서는 미분값이 작아지면서 weight값이 조금씩 업데이트됨을 예상할 수 있다. 그런데 만약 극소점이 아닌 곳에서 미분값이 0이 되어버린다면? 다시말해 local minimum에 빠지게 된다면? 학습은 더이상 진행되지 않게 된다. 그러면 이 모델은 under-fitting이 될 수 밖에 없다.
4. Optimizer의 종류
위에서 GD의 문제점에 대해 얘기했다. Stochastic gradient descent부터 많은 딥러닝 개발자들이 무지성으로 사용하는 Adam까지 많은 종류의 Optmizer가 GD의 문제점을 보완하기 위해 개발되었다.
Batch Gradient Descent
BGD? 이게 머야?라고 생각 할 수 있습니다. 일반적으로 우리가 사용하는 GD가 BGD입니다.
도대체 무슨 말이야?
딥러닝은 컴퓨터, 정확하게는 GPU로 학습하게 됩니다. 학습을 위해서는 학습 데이터를 GPU의 메모리에 올리고 메모리에서 데이터를 가져와서 학습하게 되는데 데이터의 양이 많아 지게되면 모든 학습데이터를 GPU의 메모리에 올릴 수가 없습니다. 그래서 나온 개념이 batch! batch란 간단하게 데이터를 일정크기(batch size)만큼 쪼갠것으로 딥러닝 모델은 각 batch마다 학습하여 최종적으로 모든 batch의 데이터로 cost function을 구하여 데이터를 update하는 방식으로, 정리하면 BGD란 GPU장비의 한계로 개발된 기술로 일반적으로 말하는 GD와 BGD는 동일한 기술입니다.
Stochastic Gradient Descent
SGD는 GD와 수식은 동일하며 단지 업데이트 하는 방식이 다른 기술입니다. 앞서 학습속도가 매우 느리다는 GD의 단점을 보완하기 위해 나온 기술로, BGD를 설명할때 batch단위로 끊어서 업데이르한다고 하였는데 SGD는 매 batch마다 cost function을 재설정하여 업데이트 하는 방식입니다.
BGD랑 머가 다른데?
BGD의 경우에는 모든 batch의 데이터를 계산후에 모두 더한후, parameter를 한번 업데이트 하게됩니다. 그러나 SGD의 경우에는, 매 batch마다 cost function으로 계산하여 업데이트하는 방식입니다.
데이터가 많아질수록 그만큼 업데이트가 빠를 것이고 GD보다 global minimum에 빠르게 접근할 수 있습니다. 그러나 여기에도 치명적인 문제가 있습니다.
첫번째, 학습 방향이 너무 급격하게 변한다.
두번째, 하나의 parameter에 너무 의존적이다. SGD는 learning rate에 따라 빠르게 변할수도 늦게 변할 수도 있기에 learning rate에 너무 의존적이게 되어 learning rate마다 성능차이가 심하게됩니다.
Momentum Optimizer
모멘텀은 위의 SGD에서 발생하는 문제점을 해결하기 위해 개발된 기술로 개념은 간단합니다. SGD수식과의 비교를 통해 이해를 해봅시다.
\[w_{t+1} \quad=\quad w_{t} - \eta \nabla w J(w_{t})\] \[w_{t+1} \quad=\quad w_{t} + V_{t}\] \[V_{t} \quad=\quad m\times V_{t-1} - \eta \nabla w J(w_{t})\]미분 term을 비교하면 MO의 경우, 이전에 사용했던 미분값을 추가로 더해줌으로써 이전 step에서 미분값이 컸다면 큰값을 업데이트해주며, 미분값이 작다면 작은값을 업데이트 해주게된다.
이런 의문을 가질수 있다. SGD랑 다른게 없잖아?
그렇게 생각할 수 있습니다. 그러나 이전에 사용했던 미분값을 사용하여 미분값을 업데이트하여, 함수의 기울기가 급격하게 변한다 하더라도 이전에 계산해놓은 값으로 인해, local minimum에 빠질 확률이 줄어듭니다. 그렇기에 SGD와 비교해 학습방향이 다소 완만해지며, learning rate에 크게 영향을 받지않고 학습을 할 수 있습니다.
Nesterov Accelerated Gradient
NAG는 MO을 개량하기 위해 개발된 기술입니다. 만약 global minimum근처가 매우 sharp하다는 가정을 해봅시다. MO의 경우에는 관성 term의 영향으로 인해 global minimum근처를 계속해서 왔다갔다하면서 학습시간이 불필요하게 늘어납니다. 빠른 이해를 위해 비유를 하나 하면, 어떠한 계곡의 제일 낮은 지점에 공을 안착시키고 싶다고 합시다. GD의 경우에는 일정 step만큼만 이동을 하여 계곡의 최저 지점에서 멈추게 되지만 MO의 경우에는 계곡 위에서 내려오는 관성으로 인해 최저지점을 넘어가게 되고 이런 현상은 계곡이 가파를수록 지속될 것입니다.
\[V_{t} \quad=\quad m V_{t-1} - \eta \nabla w J(w_{t} - m V_{t-1})\]이를 해결하기위해 NAG가 개발되었습니다. MO와 NAG의 수식을 비교해봅시다. MO의 경우, momentum term에 현재의 미분값을 넣어서 미래의 미분값을 계산하게됩니다. 그러나 NAG의 경우에는 momentum으로 이동한 지점의 미분값을 넣어서 미래의 미분값을 구하여 업데이트하게 됩니다. 다시말해 MO는 현재에서 미래의 값을 구하여 업데이트하지만 NAG의 경우에는 현재에서 관성만큼 이동 후, 업데이트하여 이동한 지점의 미분으로 업데이트되어 이동한 위치의 미분값을 구하여 업데이트를 하게됩니다. 이렇게하면 미래에 관성만큼 이동한 거리를 알고있는 상태에서 업데이트를 진행하기 때문에, global minimum을 ocilating하거나 지나칠 확률이 현저히 줄어들게 됩니다.
정리하면 MO은 현재에서 관성과 GD로 미래의 값을 찾는다면 NAG는 현재에서 관성만큼 이동 후, GD와 함께 최종적인 미래값을 구한다고 생각하면 이해가 쉬울것입니다.
Adaptive Gradient Descent
지금부터는 learning rate를 조절해가면서 학습하는 방법에 대해 설명하겠습니다. AGD는 learning rate에 지나치게 의존적이게 된다는 SGD의 단점을 보완하기 위해 개발되었으며, 수식을 보면서 설명 하겠습니다.
\[w_{t+1} \quad = \quad w_{t}-\frac{\sqrt{G_{t}} + \epsilon}{\eta} \nabla w J(w_{t})\] \[G_{t} \quad = \quad G_{t-1} + (\nabla w J(w_{t}))^{2} \quad = \quad \sum_{i=1}^{k} \nabla w_{t} J(w_{i})\]learning rate update term(\(G_{t}\))을 보게되면 과거의 미분값을 계속해서 더해줌을 알 수 있습니다. 다시말해 과거의 미분값이 크면 클 수 록 \(G\)가 커지면서 learning rate를 줄이는 식으로 업데이트함을 알 수 있습니다.
머야… 이거 좋은거 맞아? learning rate가 줄어들면 업데이트가 느려지는거잖아!!!
최근 딥러닝은 과거의 딥러닝 모델보다 더 많고 더 다양한 hyper-parameter를 지니게 됩니다. 그러나 모든 parameter를 동일하게 업데이트하고 학습하게된다면 좋은 성능의 모델 생성이 힘들 수 있습니다. 왜냐하면 각각의 parameter가 최적의 값을 찾아야하는데 동일하게 업데이트되는 것이 오히려 성능을 저하시키는 요인이 되기때문입니다. 또한 학습이 완료된 parameter가 있다고 하여도 동일하게 학습되면 잘 설정되어있던 parameter도 변할 수 있습니다. 그렇기 때문에 learning rate term을 두어, 학습이 많이 진행된 parameter에 대해서는 learning rate를 줄여 학습을 더디게 하고 학습이 거의 진행되지 않은 parameter에 대해서는 learning rate를 크게 만들어 학습속도를 빠르게 가져가는 것입니다.
Root Mean Square Propagation Optimizer
앞서 Adagrad에 대해 설명하였습니다. 그러나 이런 Adagrad에도 문제점이 존재합니다. 학습이 많이 진행된 parameter는 learning rate를 줄여 학습속도를 줄이는 컨셉은 좋으나, 학습이 오래되어 버린다면 뒤의 learning rate term이 계속해서 증가하여 나중에는 값이 업데이트되지 않는 현상이 발생합니다. 다시말해 학습데이터의 양이 많고 적절한 성능까지 많은 학습을 요한다면 오히려 마지막은 학습이 진행되지 않을 수 있다는 것입니다. RMSprop는 위의 Adagrad의 단점을 보완하기 위하여 개발되었습니다. 개념은 간단합니다. 아래의 수식을 보시겠습니다.
\[G_{t} \quad = \quad \gamma G_{t-1} + (1-\gamma)(\nabla w J(w_{t}))^{2}\]learning rate term에서 기존의 미분텀과 업데이트될 미분텀의 영향을 분산하며 과거의 정보는 다소 적게 반영하여 최신의 정보는 강하게 반영하여 현재의 상황을 보면서 학습하는 방식입니다. 그리하여 학습이 오래되어도 Adagrad에 비해 학습이 원활하게 되도록 하는 기술입니다.
Adaptive Momentum Optimizer
지금까지 이 optimizer를 위해 달려왔다고 해도 과언이 아닙니다. 대부분의 딥러닝 개발자들이 사용하는 그 유명한 Adam optimizer!!! 생각없이 그냥 사용하여도 좋은 이유는 이미 몇년전부터 많은 실험을 통해 그 성능과 효과가 입증이 되었기 때문입니다. 그러나 알고 쓰는 것과 모르고 쓰는 것은 하늘과 땅차이! 그러므로 Adam에 대해서 설명하겠습니다. 많은 개발자들이 사용해서 어려운 개념이라고 생각하기 쉽지만 이 기술도 매우 간단합니다. 바로 이전에 설명드렸던 momentum과 RMSprop의 개념을 짬뽕한 기술입니다. 수식을 보시겠습니다.
\[V_{t} \quad = \quad \alpha\times V_{t-1} - (1-\alpha)\nabla w J(w_{t})\] \[G_{t} \quad = \quad \beta G_{t-1} + (1-\beta)(\nabla w J(w_{t}))^{2}\] \[w_{t+1} \quad = \quad w_{t} - V_{t}\frac{\sqrt{G_{t} + \epsilon}}{\eta}\]momentum(V), learning rate(G) term을 각각 계산해서, learning rate를 step마다 계산하며 동시에 momentum값을 구하여 parameter를 update합니다.
5. Brand-new and Essue
논문제목 : AngularGrad: A New Optimization Technique for Angular Convergence of Convolutional Neural Networks
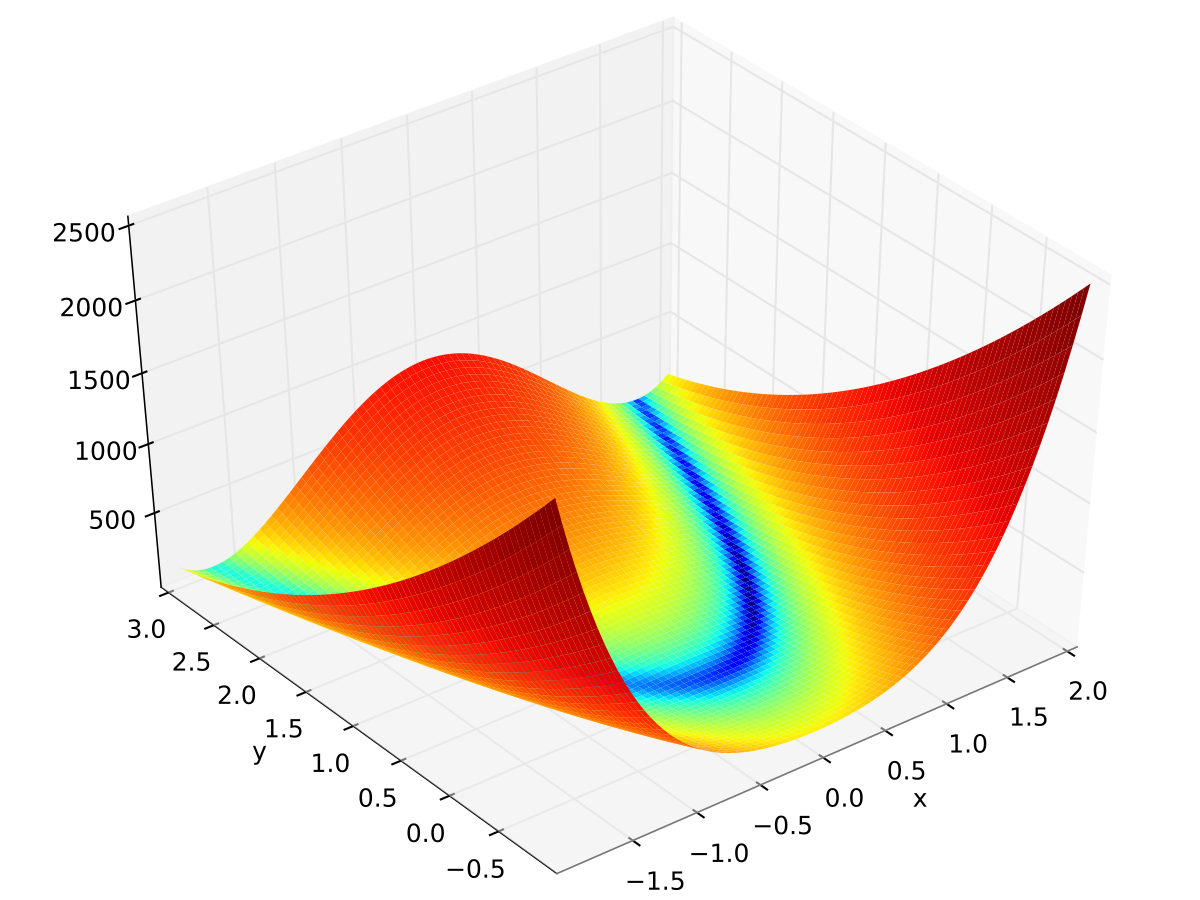
요약 : SGD부터 Adam까지 parameter-cost function그래프에서 수직방향에 대한 영향을 많이 받기 때문에, 계곡사이에 흐르는 강의 모양을 한 아래와 같은 Rosenbrock function등 다양한 최적화 알고리즘의 성능을 시험하는 함수에서 수직방향의 영향을 받아 극소점까지의 수렴이 매우 느리며 극소점 근처에서도 oscilating하는 현상이 발생하여 수직방향의 성분을 줄여 안정적으로 극소점을 찾아가는 기술에 대한 논문입니다.
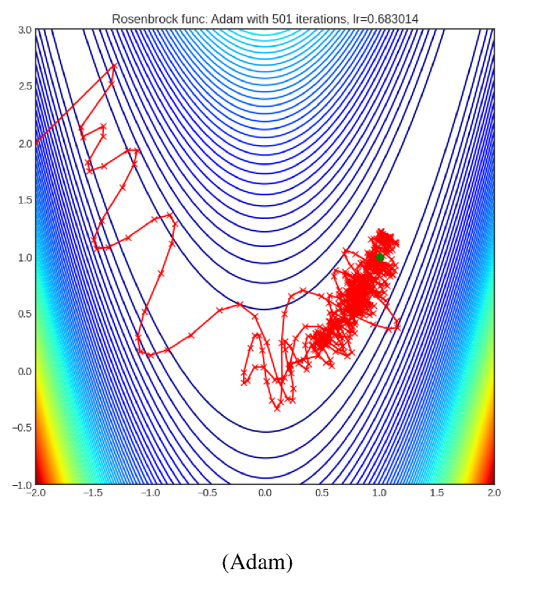
평가 : 필자는 해당 기술에 대해 다소 회의적입니다. 왜냐면 해당 논문이 2021 IEEE에 등재될정도로 우수한 논문임에는 이견이 없지만 그러한 case가 흔치 않으며 그러한 function의 극소점을 찾는 것을 사전에 알고 접근하지 않는 이상 Adam을 사용하는것이 오히려 generall하게 우수한 성능을 보장할 것이라고 생각합니다.
이슈 : SGD가 Adam보다 일반화면에서 오히려 우수하다?!
요약 : 다양한 실험을 통해 Adam의 성능이 증명되었으나 굳이 저렇게 optimizer를 복잡하게 가져갈 필요할까?라는 의문점에서 시작된 논쟁으로, Adam이 오히려 over-fitting이 가속화된다고 주장합니다. 일반적으로 Adam은 초기값 설정을 하지않아도 성능이 좋다고 하였는데 실험결과를 보니 초기값에 따라 Adam의 성능차이가 존재하였습니다. 다시말해 초기값을 어떻게 잡냐에 따라 Adam이 오히려 SGD보다 일반화에 실패하는 경우가 있다. 그러나 다른 논문에서는 딥러닝이 더욱더 딥해지면서 더 많은 parameter를 사용하기 때문에 SGD보다 Adam이 좋다고 주장합니다.
평가 : 필자는 딥한 모델을 학습시에는 Adam이 항상 SGD보다 좋다고 생각하고, 얉은 모델에서는 굳이 Adam을 고집할 필요가 있을까? 라고 생각이 되었습니다. 이렇듯 딥러닝에 대한 개발이 오래전부터 활발히 진행됬음에도 불구하고 여전히 basic한 기술과 최신의 기술에 대해 언쟁이 오가는 만큼 기초를 잘 잡고 있어야 변하는 흐름에 빠르게 대응이 가능할 것고 이런 개발자들이 시장에서 좋은 평가를 받지 않을까 싶습니다.
6. 정리
지금까지 optimizer의 개념과 gradient descent를 통해 어떤 식으로 사용되는지 확인하였고 동시에 optmizer의 기술흐름에 대해 알아보았습니다.
요약하면 optimizer는 cost function에서 weight, bias를 이용하여 이러한 parameter를 어떤식으로 수정해 나갈것인지 결정하는 알고리즘이며 이중 많이 언급되는 gradient descent는 optimizer의 개념을 이해하기 쉬운 기술로, 최초 parameter에서 cost function을 통해 값을 계산하고 이때의 미분값과 learning rate로 중학교 미분시간에 배우는 극소점을 찾아가는 과정과 동일합니다.
추가로, GD의 느린 학습속도를 보완하기 위해 나온 SGD. 그리고 여기서 momentum과 learning rate개념을 적용하여 개발된 MO와 Adagrad 그리고 극소점 근방이 sharp하거나 oscilating이 심하면 학습이 오래걸리는 MO의 문제점을 보완하기 위해 개발된 NAG. 그리고 학습이 길어지면 학습이 거의 되지않는 Adagrad의 문제점을 보완하기 위해 개발된 RMSprop. momentum과 learning rate term의 개념을 모두 종합하여 개발된 Adam이렇게 정리 할 수 있겠습니다.