Single Layer Perceptron
- 2 minsSingle Layer Perceptron
이번 포스팅에서는 모든 인공신경망의 기초가 되는 perceptron의 개념에 대해서 배워보고, 이를 이용한 단층 퍼셉트론 구조를 구현해보도록 하겠습니다.
퍼셉트론은 여러분이 고등학교 과학시간에 한 번쯤은 들어보았을 인간의 신경망, 뉴런으로부터 고안되었습니다. 퍼셉트론은 여러 개의 신호를 입력받으면, 하나의 신호를 출력합니다. 이 때 퍼셉트론이 출력하는 신호는 전달 혹은 차단이라는 1 또는 0의 값을 갖게됩니다. 직관적인 예시를 들어보도록 하죠. 여러분이 매달 초 용돈, 아르바이트비를 받거나(1) 받지 않는다(0)고 가정해보겠습니다. 여러분의 통장에 입금된 이 두 가지 수익을 input(입력) 신호라고 합니다. 이 때 여러분은 두 개의 수익이 합쳐진 통장 잔고를 확인하고 전부터 갖고 싶던 옷을 살지(1) 혹은 사지 않을지(0)를 결정합니다. 이렇게 여러분이 내리는 결정이 output(출력) 신호가 되는 것입니다.
하지만 여러분의 의사결정은 이것보다는 복잡할 것입니다. 용돈은 거의 생활비로만 사용하고, 아르바이트비를 주로 취미생활에 사용한다고 가정해보죠. 그럼 여러분이 옷을 살지 여부를 결정할 때에는 아르바이트비가 들어왔는지가 좀더 중요할 것입니다. 따라서 우리는 각 input(입력) 신호를 그대로 사용하지 않고, 각각에 가중치(weight)를 주어 output(출력) 신호를 결정하게 됩니다. 이것을 도식으로 나타내면 다음과 같습니다.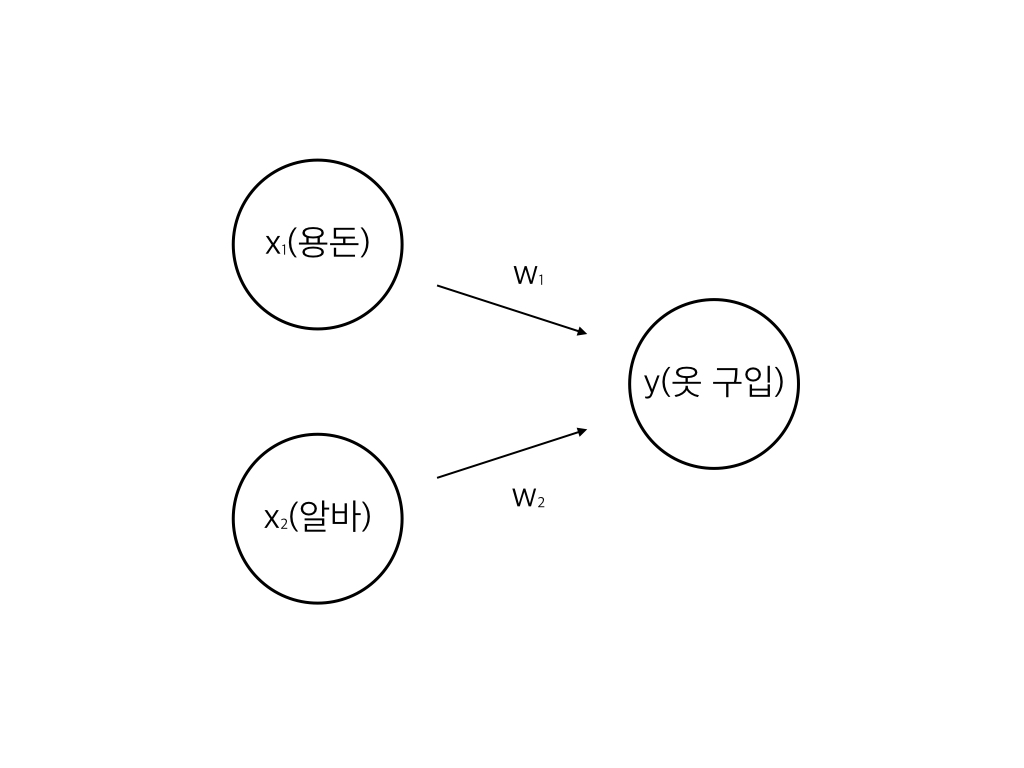 
이처럼 input에 weight가 곱해진 형태가 정해진(혹은 학습된) 임계치를 넘을 경우 1을 출력하고 그렇지 않을 경우 0을 출력하게 하는 것이 퍼셉트론의 동작 원리입니다. 정말 간단하죠! 이는 아래 수식과 같습니다.
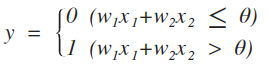
하지만 임계치를 그때그때 바꿔주는 것은 조금 직관적이지 않습니다(저만 그런가요). 그래서 우리는 아래 형태로 식을 바꾸게 되며, 이 때 추가된 b를 bias 혹은 절편이라고 말합니다.
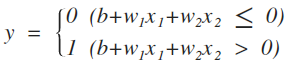
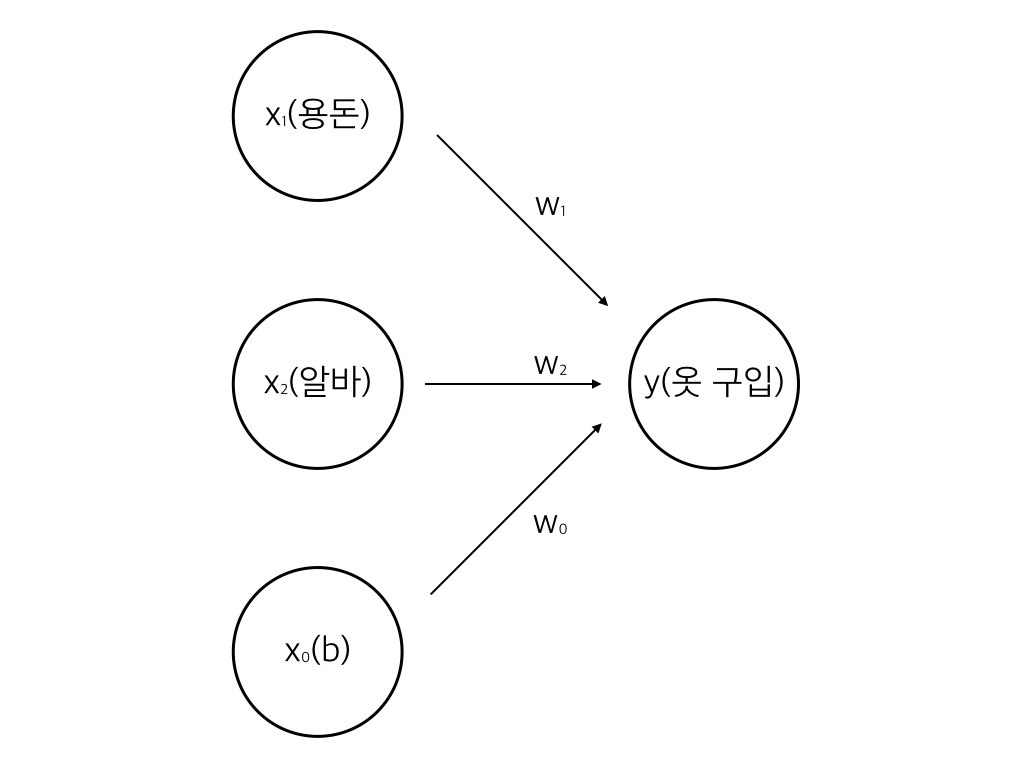
위 식은 여러분이 중고등학교 수학 수업을 잘 들었다면 굉장히 익숙한 형태일 것입니다. 바로 2차원 좌표축을 그리고 직선을 그었을 때, 그 직선을 기준으로 나뉘는 두 개의 공간을 표현한 식입니다. 역시 말보다는 그림이 이해하기 쉬울테니, 아래에 그림을 그려보도록 하겠습니다.
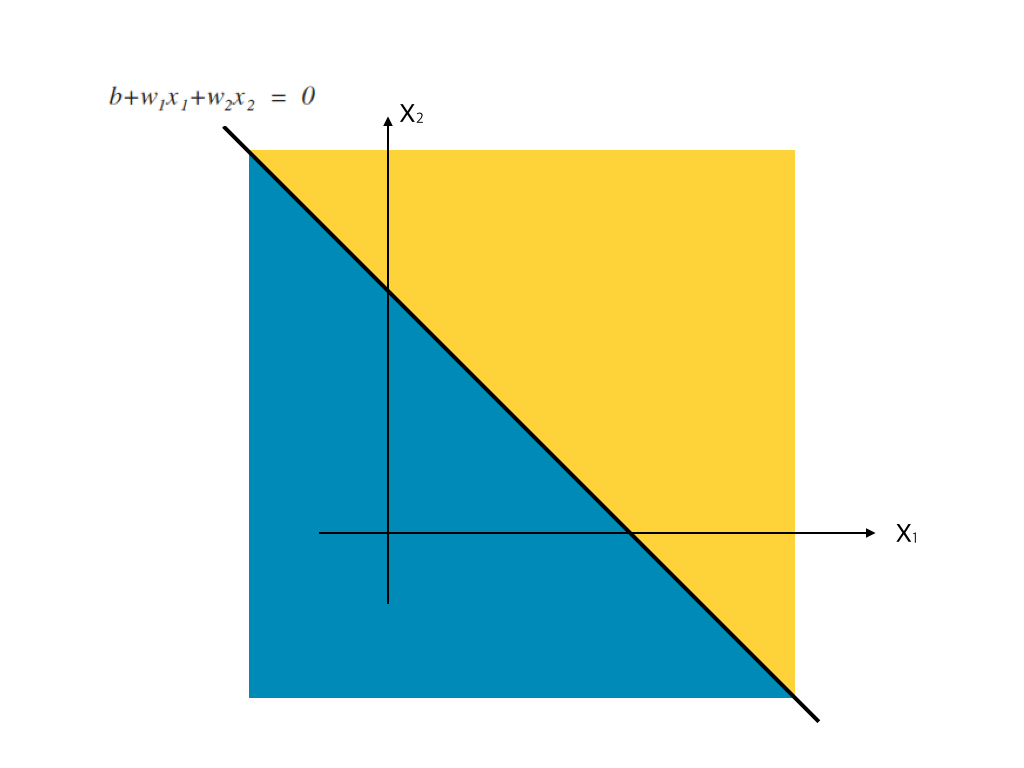
위처럼 공간을 올곧은 직선으로 나누는 것을 선형으로 나눴다고 말합니다. 하지만 직선만으로 공간을 나누는 것은 유연하지 않습니다. 위와 같은 방식으로는 OR, AND, NAND 문제는 해결할 수 있지만, XOR 문제는 해결할 수 없습니다. 이와 같은 문제를 해결하기 위해서는 층을 하나 더 쌓고, 공간을 단순한 선형이 아닌 곡선으로 분리해내어 좀더 유연한 적용이 가능해져야합니다.(사실 XOR은 선형만으로도 층을 하나 더 쌓으면 해결이 가능합니다). 이에 따라 multi layer perceptron(MLP) 의 개념이 등장하고, activation function(활성함수) 의 개념이 등장하게 됩니다. 후에 활성함수의 개념을 배우게 되면, 지금 배운 단순 퍼셉트론은 활성함수로 계단함수를 가진 것과 동일하다는 것을 알게 되실겁니다.
정리
- 단층 퍼셉트론은 모든 딥러닝 공부의 시작이다.
- 단층 퍼셉트론은 입력 신호를 받으면 임계치에 따라 0 또는 1의 값을 출력한다.
- 이러한 단층 퍼셉트론은 결국 공간을 선형으로 잘라서 구분하는 것과 동일하다.
Hyunho Cho
A team for deep learning