Vanishing Gradient

Friday. August 12, 2022 - 7 mins

Summary :

이번 시간에는 지난 시간에 다뤄 보았던 Activation Function(활성함수)과 관련된 이야기를 해 보려고 합니다. 지난 시간에는 활성함수 그 자체가 가지는 의미와 종류에 대해 알아보았다면, 인공신경망의 학습을 방해하는 Vanishing Gradient(Exploding gradient)에 초점을 맞추어 그 원인과 해결 방법에 대해 한번 파헤쳐보도록 하겠습니다! 이 글에 나오는 예시 하나하나가 인공신경망의 학습과정을 다른 각도에서 이해할 수 있는 기회가 되길 바랍니다.

Vanish? Explode?

그 전에 단어를 곱씹어 봅시다. vanish는 ‘소실되다’, Explode 는 ‘폭발하다’. 말 그대로 신경망 학습 과정에서 gradient(기울기) 값이 너무 작아지거나 너무 커진다는 의미이고, 이것은 학습에 좋지 않은 영향을 주어 성능이 저하되는 원인이 됩니다.

머신러닝에서 학습은 항상 ‘적절히’ 진행되어야 하고, gradient 값 또한 알맞게 유지되어야 parameter(모수)값이 잘 update됩니다. 인공신경망의 핵심 원리인 Backpropagation과정과 함께 직관을 얻어봅시다.

Gradient는 어떻게 계산되는 건가요?(Backpropagation)

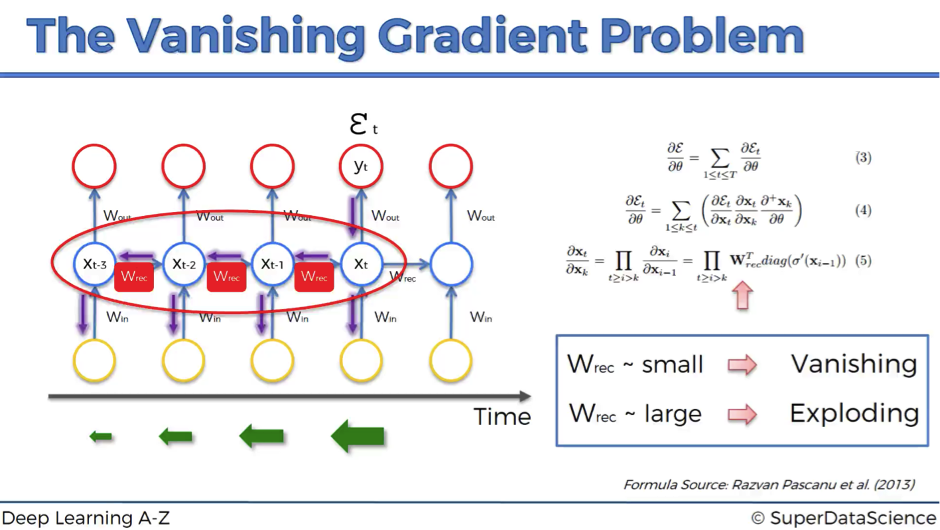
아래 그림은 Backpropagation과정을 담은 모식도입니다. 2개의 node(neuron)로부터 output을 내는 node를 거치고, Loss 값이 계산되는 구조인 Feed-Forward network의 일부라고 생각하면 됩니다. Feed-forward Network란 여러 layer로 이루어진 딥러닝의 일반적인 network를 의미한다고 이해하면 됩니다.

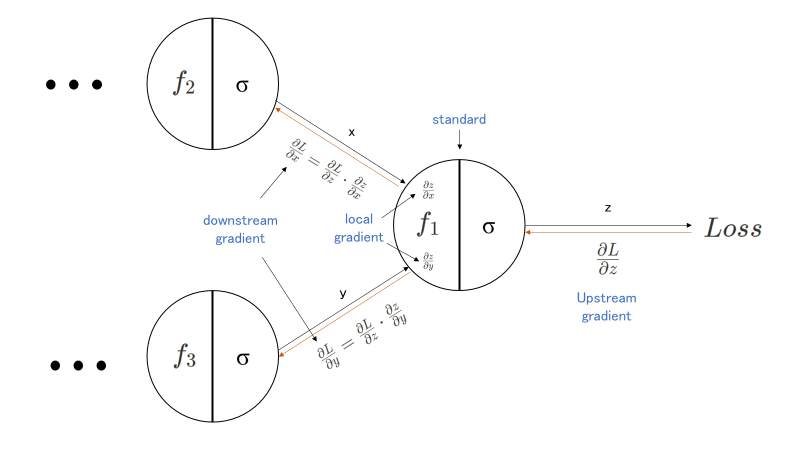
모델로 들어간 input은 여러 layer를 거쳐 마지막 f1 함수와 특정 activation function을 거쳐 z라는 output을 갖게 됩니다. 이 z는 특정 objective function(목적 함수)에 의해 Loss값이 계산되고, 이 Loss 값의 gradient(편미분 값에 의한) 계산을 통해 backpropagation이 시작되죠. 여기서 Objective Function이란, 우리가 더 학습이 잘 되도록 최적화(optimize)하는, 말 그대로 목적이 되는 함수를 의미합니다. 그렇다고 한다면, 아래 f1 함수를 포함한 마지막 노드를 기준으로 하여, 오른쪽에서 다가오는 값은 upstream gradient,그리고 내부에서 계산되는 z에 대한 x와 y의 gradient 값은 local gradient가 됩니다. 그리고 이 upstream gradient와 local gradient값을 곱하여 downstram gradient 값을 구할 수 있게 되는 데, 이것이 역방향으로의 gradient를 구하는 backpropagation의 과정으로 설명이 가능합니다.(이 과정에서 Chain Rule이 적용이 됩니다.) 다시 말해, 위와 같은 방법으로 Loss 의 초기 input 값들에 대한 gradient(정답과 멀어져있는 정도)값들을 계산할 수 있게 되고, 그 값만큼(멀어져있는 만큼)을 곱하여 parameter를 update하게 되는 것이죠!

여기서 잠깐, gradient는 벡터의 특정 변수에 대한 편미분값이자 변화율을 의미합니다. 이 상황에서는 input 벡터에 대한 Loss(output)의 변화율인 것이죠. 쉽게 말해 input과 관련해서 Loss가 변한 정도라고 이야기할 수 있겠네요! 더 깊은 수학적인 개념 편미분과 Chain Rule을 키워드로 추가 검색 및 공부를 추천드립니다.

정라하자면, input을 모델에 넣고, 여러 함수(layer)를 거쳐 Loss를 계산하고, 변화율만큼 parameter를 update해준다 라고 직관을 얻을 수 있을 것 같습니다.

그렇다면 Vanishing gradient는 어떻게 발생하나요?

그렇다면 Vanishing gradient는 어떻게 발생하는 걸까요? 답은 간단합니다. local gradient로 1보다 작은 값이 (거듭) 곱해지게 되면 점차 값이 0과 가까워지게 됩니다. Layer를 더 깊이 쌓을 수록 0과 가까워질 가능성은 더 높아질 것입니다. Chain rule, 즉 연쇄 법칙에 의해 upstream gradient의 결과물에 local gradient 값이 다시 곱해지기 때문이죠(아래 그림 참고).

반대로 1보다 큰 값이 거듭 곱해진다면, Exploding Gradient가 발생할 가능성이 크다는 사실은 똑똑한 독자라면 바로 눈치챌 수 있을 거에요!

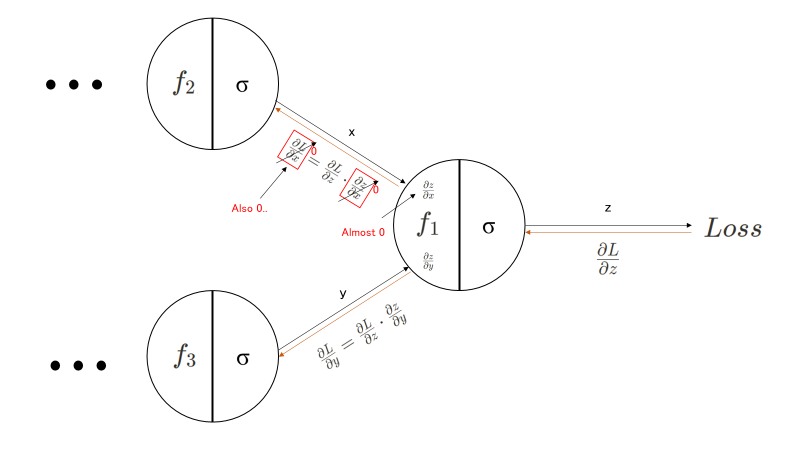
이것이 문제가 되는 점은, Loss 값(정답으로무터 떨어진 정도)에 관계없이 너무 크거나 작게 parameter가 update된다는 것이에요. Loss가 크면 큰 만큼 많이 바꾸고, 작으면 작은 만큼만 바꾸어야 학습이 잘 진행될텐데, 모델이 그것을 파악하지 못하고 제대로 update하지 않아 결국 parameter(weight) 값이 줄어들지 않는 현상이 발생하여 버리는 거죠. layer가 깊다면, 중간 layer들의 parameter는 제대로 update될지 몰라도, 초기 layer로 가면 갈수록 더 영향력이 줄어들 것이라는 것도 예상이 가능해요.

아래 그림을 보며 전체적인 과정이 감이 온다면 매우 잘 따라오고 계신 겁니다!

발생 예시

우리가 어떠한 경우에 vanishing gradient가 발생할까를 떠올려 보면, 왜 local gradient가 0이 될까? 라는 질문으로 바꾸어 생각해볼 수 있습니다. 인공신경망에서 local gradient는 반드시 특정한 함수에 nonlinear(비선형)한 activation function가(활성 함수) 결합된 형태입니다. 여기서 비선형이란 linear combination(선형 결합)으로 재생산될수 없는 함수를 의미하며, 딥러닝의 존재 의의 중 하나가 됩니다. 비선형 함수에 결합된 선형 함수는 실로 매우 다양하고, 선형 함수에 의해 vanishing gradient가 발생하는 경우는 많지 않습니다. local gradient를 0으로 만드는 것들은 대부분 활성함수이고, 아래에 소개된 것들이 그 예시입니다. 서두에 언급되었던 내용이기도 하죠!

case 1) sigmoid function

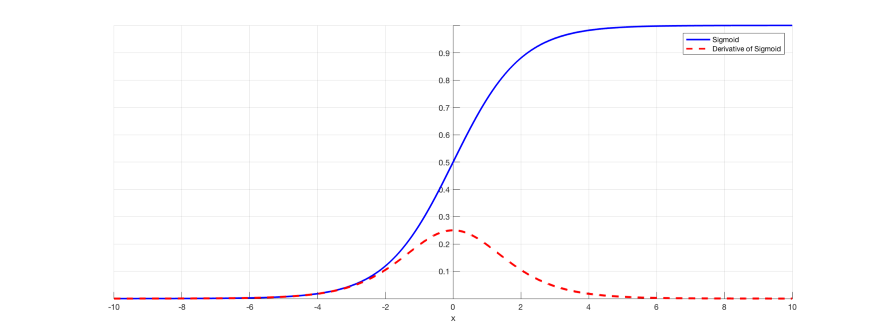
위 그림은 대표적인 sigmoid 함수와 그 도함수의 모습입니다(도함수란 그 함수의 미분값으로 이루어진 함수를 의미합니다). 도함수는 0일때 최댓값 1/4를 가지고, 0에서 멀어질 수록 더 작아지는 값을 가지게 돼요. 그것은 결국 gradient 값이 커봐야 1/4 이 된다는 의미이고, 언급한 1보다 작은 값이 되죠. downstream gradient는 결국 그 값이 작아지게 될거에요. 여러 layer를 거친다면 더더욱 작아질 것입니다.

case 2) RNN

[vanishing gradient in RNN]

Vanishing Gradient는 RNN 에서 특히 문제가 됩니다. RNN의 존재 의의인, 이전 step들의 hidden state 값이 layer를 거치며 점차 그 영향력을 잃어버리는 것이죠. 이것을 우리는 long-term dependency(장기적 의존관계)를 반영하지 못한다고 표현하고, 바로 Vanishing Gradient(또는 Exploding Gradient)가 그 원인인 것입니다.

해결 방법

1) ReLU & LeakyReLU : gradient값이 0이 되지 않는 activation function을 사용하자

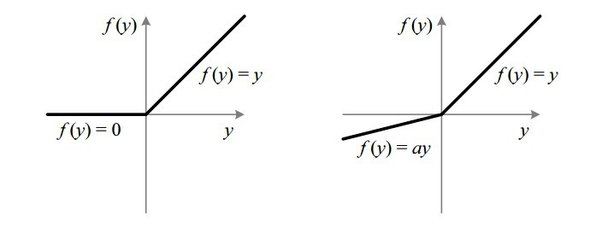
그림과 같은 다른 activation function을 활용하는 것이 기본적으로 vanishing gradient 문제를 해결하는 데에 도움이 됩니다. ReLU 함수는 input이 커져도 gradient 값이 1로 대응되기 때문에, Loss 값을 보다 잘 보존할 수 있게 됩니다. 하지만 음수 값이 input으로 들어올 경우, 값이 0으로 대응되어 회복되지 않는 dying RELU 현상이 일어나기 때문에 오른쪽 그림과 같은 Leaky ReLU로 보완하는 방법도 있습니다.

2) RNN -> LSTM! : 새로운 모델을 고안하자

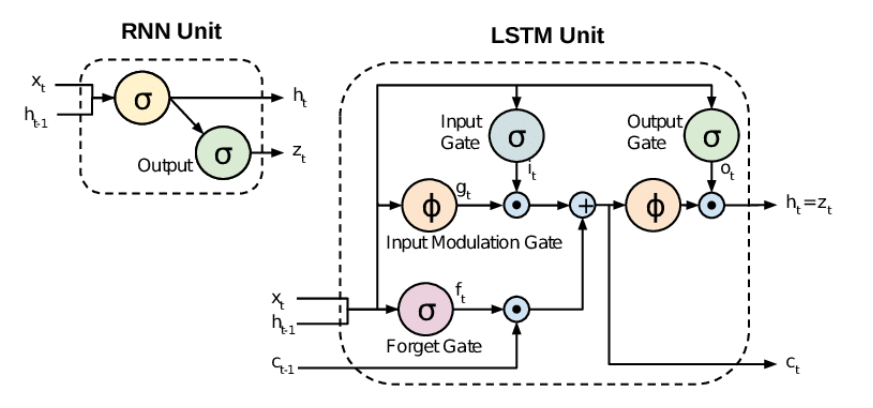
기존 vanishing Gradient issue를 해결하기 위해 RNN계열의 발전된 모델인 LSTM 모델이 연구를 통해 개발되었습니다. 핵심적인 개념은, 다양한 연신을 진행하는 gate들과 장기적 의존관계를 반영하는 ‘memory cell’을 추가하여 gradient 소실을 막았다는 점입니다. LSTM에 대한 자세한 내용은 논문을 비롯한 다양한 연구 자료를 참조하시면 더 이해가 잘 되실 겁니다.

3) Residual Network : 함수를 거치지 전 input을 더해서 소실을 완화하자

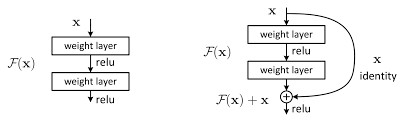
인공신경망, 특히 Computer Vision의 핵심 모델인 CNN(Convolutional Neural Network)의 발전 과정 중, layer수가 늘어날수록 오히려 학습이 제대로 진행되지 않는 현상이 발생하여 고안된 방법론입니다. ResNet이 학계에 가져온 혁신에 비해 원리는 매우 간단합니다. gradient를 0으로 만드는 것은 대부분 activation function을 거친 이후이기 때문에, input으로 들어오던 x를 layer를 거친 F(x)(함수의 output)와 더해주어 output을 산출합니다(그림 참고). 결과적으로 F(x) 값이 0과 가까워져도, x 값이 남아있어 gradient값을 적정하게 유지시켜주는 역할을 하는 것입니다.

4) Proper Weight initialization : 초깃값을 적절히 설정하자

인공 신경망에서는 초기 parameter(weight)값을 설정을 해주어야 연산 및 학습을 진행할 수 있습니다. 학습을 진행할 때 초기 weight값을 0으로 설정하여 버리면, gradient 가 모두 똑같은 값으로 적용되어 버리는 현상이 나타납니다(위의 backpropagation 과정으로 이해해 봅시다). 이는 결국 인공신경망의 nonlinearity를 활용하는 의미가 사라지는 셈입니다.
이와 더불어 vanishing Gradient를 막기 위해서는 아래와 같은 조건을 따라야 한다고 합니다.

각 layer output의 분산(variance)값이 input의 분산값과 유사해야 함.
backpropagation 시 각 layer의 upstream gradient와 downstream gradient값이 같아야 함.

정규분포로 생성하는 Xavier Initialization, uniform 한 분포로 생성하는 Glorot initialization 등 다양항 기법이 있으며, 적절한 기법을 선택하는 것이 중요합니다.

5) Batch Normalization : node들의 input의 분포를 균일하게 하여 격차를 줄이자

이제 vanishing gradient를 하나의 input이 아닌 여러 input의 관점에서 바라봅시다. input이 여러 개라면 큰 값도 있고, 작은 값도 있을 것입니다. 우리가 지속적으로 이야기하는 parameter update가 잘 이루어지려면 이 분포에 대한 정비도 해 주어야 합니다. 그렇지 않으면 어떤 값은 0, 어떤 값은 explode 되어 의도한 결과가 나오지 않을 것이기 때문입니다. 이는 training 속도를 늦추고, learning rate와 같은 hyperparameter에 대한 자유도를 낮추고, initialization도 더 섬세하게 진행할수 밖에 없게 만들죠(nolinearity saturation).

다시 말해 weight initialization, activation function 개선 등에도 학습 도중 예측할 수 없는 gradient 소실 문제가 발생할 수 있다는 이야기입니다.

batch normalization은 신경망의 node들의 input의 distribution을 조정해주는 기법입니다. 각 minibatch 안의 input을 normalize해주고, 학습 parameter를 통하여 scaling(크기 조정) & shifting(평행 이동)을 학습 시 진행하여 줍니다. 마치 고등학교 때 배웠던 Z분포 변환을 기억하여 이해해보면 좋을 것 같습니다.

이러한 함수를 추가함으로서, gradient 의 분포를 조정하여 전체적으로 적절한 값으로 유지시켜주는 역할을 한다고 이해하면 됩니다. 자세한 내용은 논문을 참고해 봅시다!

Conclusion

이번 시간에는 Vanishing/Exploding Gradient가 일어나는 원리와 그 해결 방안에 대해 알아보았습니다.

Vanishing Gradient는 Gradient값이 유지되지 않아 parameter가 제대로 update되지 않는 현상을 의미합니다.
주로 Backpropagation에서 activation function의 영향으로 인해 Gradient가 소실되는 경우가 많습니다.
Activation function을 보완하고, 초깃값을 재설정하고, 분포를 조정하고, 새로운 모델 및 기법을 활용하는 등 다양한 방법으로 vanishing gradient를 해결 가능합니다.

이외에도 Exploding Gradient를 막기 위한 Gradient Clipping 기법 등 다양한 방법을 시도하여 gradient를 적절히 유지할 수 있습니다. 그리고 실무에서는 이러한 문제점을 보완하기 위해 pretrained model을 활용하고 목적에 맞게 customizing하는 경우도 많이 찾아볼 수 있습니다. 인공신경망은 어렵지만, 그래도 gradient를 유지하는 다양한 방법들을 고민해 보며 성능을 개선시킨다면 더 매력을 느낄 수 있을 겁니다!