Regularization
- 7 minsRegularization
뭐든 적당한게 최고
지금까지의 포스팅을 모두 읽은 사람이라면 좋은 모델 설계와 우수한 학습 방법으로 좋은 성능의 딥러닝 모델을 얻을 수 있다는 것을 알 수 있습니다. 그러나, ‘과유불급’이라는 말이 있듯 이전 포스팅에서 학습을 과도하게 많이하면 오히려 성능이 떨어지는 over-fitting에 대해 설명하였습니다. 그리고 대부분의 딥러닝 개발자들이 under-fitting보다 over-fitting에 대한 문제를 해결하기 위해 많은 리소스를 할애합니다.
왜? 그냥 학습데이터 많이 사용하면 되잖아!
사실 맞는 말입니다. 그러나 단순히 학습데이터의 양만 많다고 해서 좋은 모델을 개발할 수 있는 것은 아닙니다. 중요한 것은 학습데이터의 질입니다. 그러나 대부분의 질 좋은 학습데이터는 기업에서 소유를 하고 자신들만이 사용하려 하기 때문에 일반적인 개발자들은 질 좋고 많은 양의 데이터를 사용하기가 매우 어렵습니다. 그래서 적은 양의 데이터와 낮은 품질의 데이터로 우수한 성능의 모델을 생성해야하기에 개자들이 over-fitting해결에 좀더 집중을 하고 있는 이유입니다. 그리고 이런 over-fitting을 해결하기 위한 대표적인 방법이 regularization기법입니다.
이번 포스팅은 아래와 같은 순서로 진행합니다.
- What is Regularization?
- Norm
- L1, L2 regularization
- 정리
- reference
1. What is Regularization?
Regularization은 통계에서도 많이 사용되는 단어로 ‘일반화’, ‘정규화’라고도 불리웁니다. 일반적으로 머신러닝은 과도하게 학습이 되면 오히려 성능이 떨어지는 경우가 발생합니다.
머신러닝이 정답 잘 맞추도록 학습하는 거아니야? 대체 무슨 말이야?
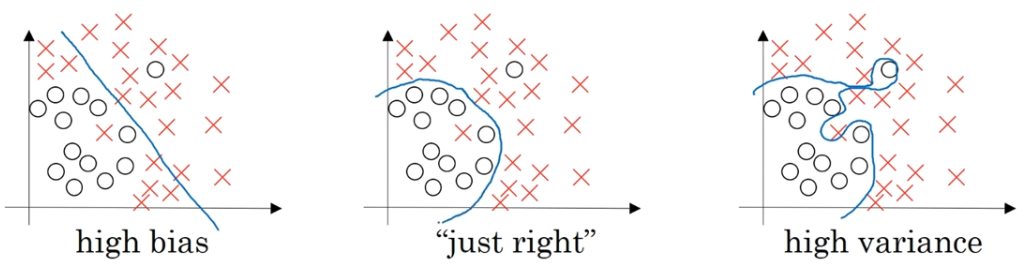
이전 포스팅에서 언급했듯 특정 데이터에 대해서만 과도하게 학습했기 때문에 동일하지 않은 비슷한 문제에 대해서는 낮은 성능을 보이는 현상을 over-fitting이라고 하였습니다. 아래 그림을 보며 설명을 하겠습니다. 첫번째 그림은 high bias이며 이 경우는 일반적으로 under-fitting을 의미하며, 세번째 그림은 high variance이며 over-fitting의 경우를 얘기합니다.
세번째 그림이 정답을 잘 맞추는 모델 아니야?
그렇게 보일 수 있습니다. 그러나 학습데이터와 유사하지만 학습데이터로 사용되지 않는 데이터가 입력으로 들어오게되면, 과도하게 학습된 모델은 해당 데이터를 제대로 인식하지 못하는 문제가 발생합니다. 그래서 여기에 regularization을 적용하여 두번째 그림처럼 약간의 오차가 있지만 대부분의 데이터에 대해 우수한 성능을 내는 모델이 엔지니어들이 일반적으로 생각하는 좋은 모델입니다.
그러면 머신러닝 분야에서는 regularization을 어떤식으로 적용하여 모델을 일반화시킬까요?
2. Norm
먼저 regularization을 설명하기 전에 알아야할 것이 있습니다. 바로 Norm이라는 것입니다. Norm이란 벡터의 크기를 계산하는 방법입니다. 수식은 아래와 같습니다. 다양한 종류의 norm도 많지만 여기서는 L1, L2 norm에 대해서만 설명을 드릴려고합니다.
L1 Norm & Loss
아래의 수식을 보면서 설명하겠습니다. L1 norm은 각 원소의 절대값의 합으로 계산되며, ‘manhattan distance’, ‘texicab geometry’이라고도 불리읍니다. 아래의 수식은 어떤 의미를 얘기할까요? 예를 들어 설명하겠습니다. 우리가 빌딩 숲을 지나서 목적지로 간다고 가정을 해봅시다. 1이 도로의 한 블럭을 의미한다고 가정하고, 현재 위치가 (-5,4) 목적지가 (3,10)이라고 가정을 하면 |-5-(+3)| + |4-(+10)| = 14 즉 어떤 방향으로 가든 총 14블럭을 이동해야 목적기에 도착이 가능합니다. 이제 manhattan distance라는 의미가 이해가 가시나요? 맨하탄에서 각 블럭을 1로 두고 목적지까지의 거리를 계산하면 L1 Norm처럼 계산하면되기 때문입니다.
\[||x_{1}|| \quad=\quad \sum_{i=1}^{n} |x_{i}|\]그러면 여기서 나아가서 L1 loss는 무엇일까요? 수식의 \(y_{true}\)는 정답값 \(y_{pred}\)는 예측값입니다. 수식을 설명하면 정답값과 예측값의 거리를 L1 norm방식으로 계산하겠다는 의미입니다.
\[L1 \ Loss \ Function \quad=\quad \sum_{i=1}^n |y_{true} - y_{pred}|\]L2 Norm & Loss
L2 norm은 각 원소의 제곱의 합을 루트로 씌운것으로 기하학에서는 euclidean distance라고 불리웁니다. 아래의 수식을 L1에서 사용한 예를 가져와서 적용하면 \(\sqrt{(-5-(+3))^2 + (4-(+10))^2} = 10\). 즉 목적지까지 직선으로 갔다는 가정하에 10블록의 거리를 가면 목적지에 도착한다는 의미입니다.
\[||x_2|| \quad=\quad \sqrt{\sum_{i=1}^{n} x_{i}^{2}} \quad=\quad \sqrt{x^{T}x}\]L1과 동일하게 L2 loss는 무엇일까요? 아래의 수식을 설명하면 정답값과 예측값의 거리를 L2 norm방식으로 계산하겠다는 의미입니다.
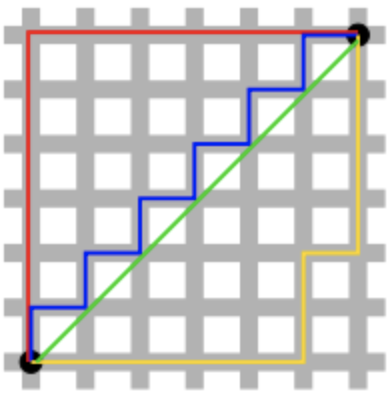
\[L1 \ Loss \ Function \quad=\quad \sum_{i=1}^{n} |y_{true} = y_{pred}|\]아래의 그림을 보면 L1, L2 norm의 의미를 쉽게 이해할 수 가 있습니다. 초록색이 L2 norm, 나머지 선들이 모두 L1 norm을 의미합니다. 아래 그림에서 보이듯 L2 norm은 오직 하나의 값만을 지니며, L1 norm은 여러 값이 존재할 수 있는 것입니다.
L1, L2 Loss의 장단점
L1, L2 loss의 장단점은 무엇이 있을까요? 먼저 L2의 경우, 제곱의 합을 root취한 것이기 때문에 outlier가 들어오게되면 loss값의 변화가 큽니다. 반면에 L1의 경우, 절대값의 합이기 때문에 L2에 비해 outlier에 강인한 모습을 보입니다. 반대로 말하면 L2의 경우, outlier가 나오게 되면 빠르게 반응하여 stable하게 loss를 모델에 전달 할 수 있으며, L1의 경우 outlier에 둔감하여 unstable한 특성을 지니게 됩니다. 그래서 outlier의 반영을 크게 하고 싶다면 L1 loss를 쓰는것이 좋고, outlier를 무시하면서 stable하게 학습하고 싶다면 L2 loss를 사용하는것이 모델 학습에 좋은 영향을 미칩니다. 또한 일반적으로 모델은 안정적으로 loss를 받는 것이 학습에 좋기 때문에 L2 loss를 많이 사용합니다.
그럼 여기서 조금 더 나아가서 L1, L2 regularization에 대해 설명하겠습니다.
3. L1, L2 regularization
우선 각각의 방법을 설명하기 전에 OO번째 포스팅된 cost function 부분을 읽고 오시길 권장드립니다.
머신러닝에 자주 사용되는 regularization에는 다양한 방법이 존재하지만,일반적으로 머신러닝에서 얘기하는 regularization은 L2-regularization을 의미하는 것이기에 L2에서 L1순으로 설명하게습니다. 추가로 L2-regularization이 머신러닝에서 많이 이유에 대해서도 설명하겠습니다.
L2-regularization
아래의 수식을 보면 기존의 loss function에 L2 norm을 더한 것이 L2-regularization임을 알 수 있습니다. L2 norm term이 어떤 영향을 줄까요? 이전에 loss function은 미분을 통해서 w값을 업데이트한다고 설명하였습니다. 그러면 위 수식에서 weight에 대해 편미분을 진행하면 아래와 같은 수식이 완성됩니다. Back-propagation과 single L2 norm으로 말이죠 이 수식을 weight를 업데이트하는 2번 수식에 넣어서 정리하면 기존방법에 비해 L2 regularization은 weight가 감소하는 방향으로 업데이트 함을 알 수 있습니다.
\[Loss \quad=\quad Error(y, \hat{y}) + \lambda \sum_{i=1}^{N} w_{i}^{2}\]L1-regularization
아래의 L1수식을 통해 loss function에 L1 norm이 더해진 것이 L1 regularization인 것을 알 수 있습니다. L2와 동일하게 loss function을 weight에 대해 편미분을 하고 기존 방법과 비교하면, L1 regulariation은 이전 step weight의 상수값을 계속해서 빼주는 것을 알 수 있습니다. 그래서 정리하면 L1-regularization은 특정 상수값을 weight update과정에서 빼주는 것을 알 수 있습니다.
\[Loss \quad=\quad Error(y,\hat{y}) + \lambda\sum_{i=1}^{N}|w_{i}|\]L1, L2 regularization의 공통점과 차이점
공통점과 장점
regularization관점에서 L1, L2는 무엇이 어떻게 같고 다를까요? 우선 L1, L2 모두 cost function을 통해 weight를 update할때, weight가 작아지도록 update를 하게 됩니다.
그러면 이런 방법이 모델에 어떤 영향을 미칠까요?
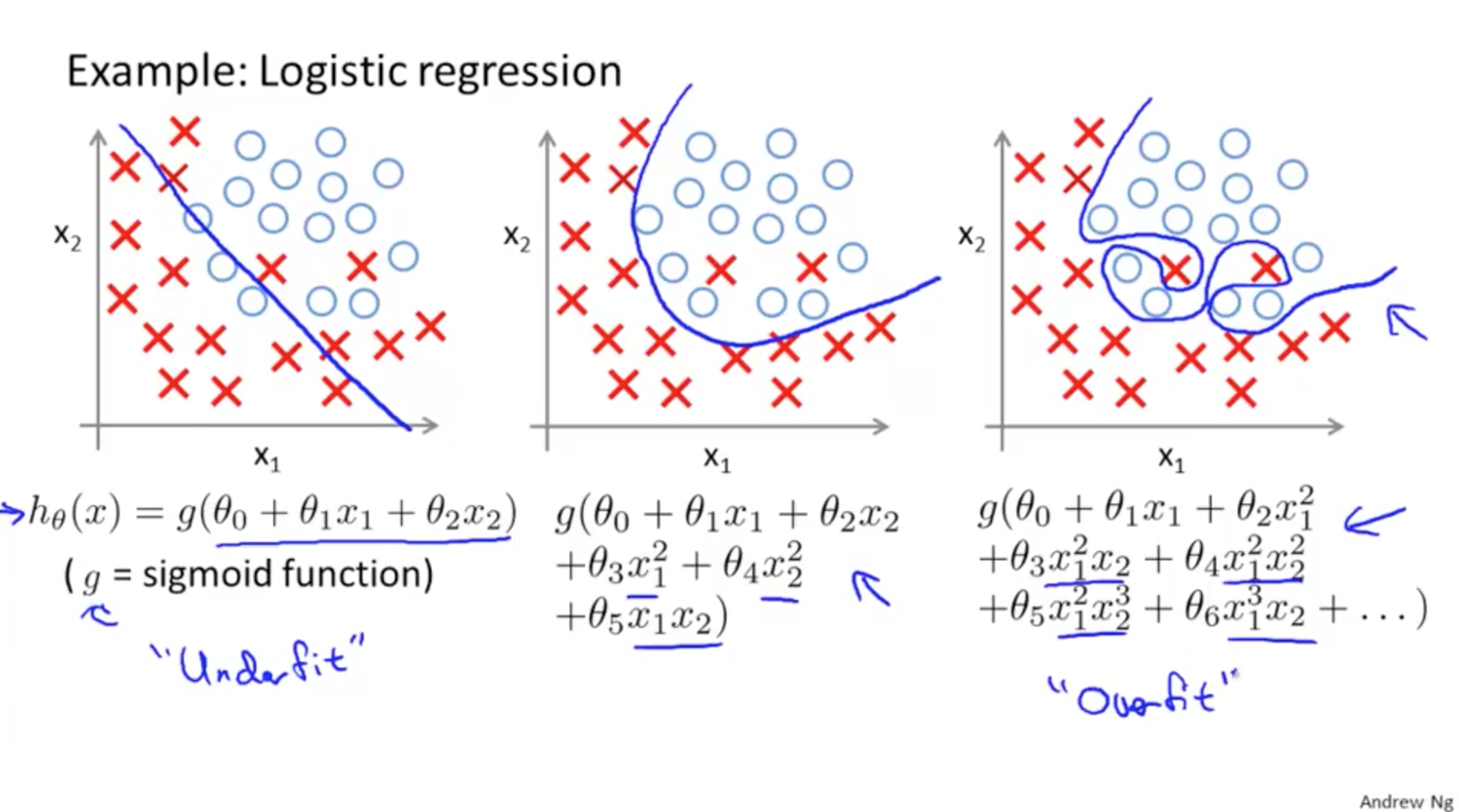
바로 일반적인 case를 위한 안정적인 모델을 생성하겠다는 의미가 됩니다. local값 혹은 outlier가 갑자기 큰값을 지니고 regularization이 없다면 local값에 따라 가중치가 높은 feature들은 계속해서 강조가 되고 그렇게 되면 아래의 세번째 그림처럼 overfitting이 일어나게 되는것입니다. 그래서 regularization을 통해 weight를 적정수준으로 낮춰주는 작업을 통해 모델 일반화를 진행하게 되는 것입니다.
regularization을 통해 weight를 낮춰주게 되면 또 다른 장점이 발생하게 됩니다.
첫번째, weight의 값들이 골고루 분포하게 됩니다. 아래의 그림처럼 특정 weight만 너무 강조되었을 경우, 낮은 성능의 모델이 생성되고 다수의 고차원 weight들이 존재하게 될경우 overfitting의 문제점이 발생하지만, regularization와 regularization-parameter의 조절로 적정수준의 weight를 남겨두어 모델 일반화를 진행하게 됩니다.
두번째, activation function관점에서도 weight가 낮아지게된다면 모델 일반화가 가능하게 됩니다. 예전에 많이 사용되었던 activation function을 보시면, z = wa +b의 꼴입니다. 그리고 w가 작아지게 된다면 z는 선형부분에서 update를 진행하게 됩니다. 그렇게 되면 각 layer가 선형적인 특성을 지니고 나아가 전체 모델도 선형적인 특성을 지닌 모델이 됩니다. 그러면 반대로 이런생각을 하실수 있습니다.
‘머신러닝이 비선형적인 문제를 잡으려고 개발되는 기술인데 저렇게 되면 성능이 안좋은거 아닌가?’ 어느정도 맞는 얘기입니다. 그러나 여기서 얘기하는 수준은 과도하게 학습되어 학습한 데이터만 예측하는 수준보다는 일반화를 시켜야지 좋은 모델이 된다는 가정하게 개발된 기술이며 현재 많은 머신러닝 개발자들이 해당기술을 통해 성능 증가를 확인했기에 무턱대고 사용해도 될 정도로 이미 성능이 보장된 기술입니다.
차이점
그러면 L1, L2는 어떻게 다를까요?
먼저 L1의 경우, 위에서 얘기했듯 update마다 이전 step의 상수값만큼 줄여준다고하였습니다. 그래서 학습되는 과정에서 너무 낮은 값의 weight의 경우, 0이 되는 경우가 발생합니다. 그래서 정말 중요한 weight를 제외한 나머지 weight의 경우, 없어지게 됩니다. 그래서 일반적으로 데이터와 모델을 통해 중요한 feature를 분석할때 L1을 사용하거나, 모델을 압축할 때 L1을 많이 사용한다고 합니다.
L2의 경우, 값이 작아지긴하지만 L1처럼 상수값을 계속 빼주는 것이 아니라 step이 지날수록 n이 증가한 값을 빼주기 때문에 weight들이 전반적으로 작은 값을 가지게 되고 동시에 낮은 가중치값들도 0이 되지않고 작은 값으로 남아있게 됩니다. 그래서 모든 weight들이 고루 분포하게 되고 이를 도식화하게 되면 위의 두번째 그림처럼되는 것입니다. L1도 두번이런 이유때문에 머신러닝이 L1 regularization보다 L2 regularization을 사용하는 이유입니다.
6. 정리
이번 포스팅에서는 regularization에 대해 설명하였습니다.
포스팅요약을 하면, 첫번째 regularization은 모델 학습과정에서 weight를 작은 값으로 update하게하여 모델 일반화를 통해 학습데이터 이외의 데이터에 대해서도 우수한 성능을 내도록 해주는 기술입니다.
두번째, L1의 경우 상수값을 빼주면서 weight를 update하기 때문에 큰 값의 weight를 제외한 나머지 weight의 경우, 0으로 만들어 모델을 압축하는 효과를 줍니다. 그리고 L2의 경우 weight를 regularization/N의 값으로 계속 감소시켜 전반적인 weight를 줄여주며 0이 아닌 값을 지닌 weight를 생성하게 하여 L1보다 안정적으로 모델을 학습시켜 나갈 수 있습니다. 이 2가지만 확실하게 알아가시면 이번 포스팅을 훌륭하게 이해하신 것입니다.
7. reference
youtube link
- https://youtu.be/6g0t3Phly2M
- https://youtu.be/NyG-7nRpsW8
blog
- https://m.blog.naver.com/laonple/220527647084
- https://wooono.tistory.com/221